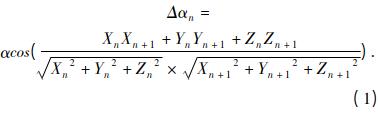摘 要: 文章探讨了对液位变送器静态角度进行高精度测量的方法。该方法在两台经纬仪观测数据的基础上利用双站交会算法计算各被测点的空间三维坐标,据此得出液位变送器静态旋转角度。文章还利用 Matlab 和数学仿真的方法对测量误差进行了计算分析,提出了改进措施。zYw压力变送器_差压变送器_液位变送器_温度变送器
引言
随着科技的进步和设备自动化需求的提升,液位变送器被越来越广泛地应用于光电跟踪、武器发射、安全监控等各个技术领域,对液位变送器定位角度的精度要求也越来越高,往往需要精que到角分级。典型的液位变送器一般同时具备方位和俯仰两套回转机构,分别用于实现方向和高低的角度定位。对这两个方向进行静态角度测量,以确定装置的定位精度是该类设备调试和试验过程中必须进行的工作。本文提出了一种实用且通用的液位变送器静态角度测量方法,并对它的测量精度进行了核算。
1 原理
1. 1 概述
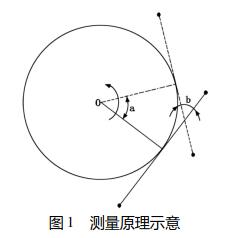
如图 1 所示,当一个旋转体转过角度∠a 时,旋转体上的某一条切线转过∠b。可以知道∠a = ∠b,也就是说,只要测得∠b,也就得到了该旋转体实約hou慕嵌取?/div>
2 测量误差分析
测量误差主要由仪器误差、架设误差、观测误差、计算误差等几个部分组成。其中计算由软件完成,所有变量取双精度浮点数,因此计算误差可以忽略不计。其它三部分误差对计算结果的影响均体现在对被测点的观测和定位上[3]。
仪器误差即所用的经纬仪的测角精度,为 2" 。观测误差由人工瞄准造成,属于随机误差,每次均不相同。所使用经纬仪#小刻度为 1" ,则观测误差#大为 0. 5" 。
架设误差属于系统误差,架设完成后进行测量时不会变化。在计算过程中,架设误差体现为公式( 2) 中的( x1 ,y1 ,z1 ) 和( x2 ,y2 ,z2 ) 。通常设经纬仪一位于坐标原点,即( x1 ,y1 ,z1 ) 恒等于( 0,0,0) ,y2未出现在公式中,所以只需考虑 x2 和 z2 的影响。架设时两台经纬仪间进行对觇标定,可设经纬仪二位于以经纬仪一为原点的坐标系的 X 轴上。则 x2即为两台经纬仪间的直线距离,z2 = 0。但由于仪器误差和观测误差的存在,z2 可能实际上不为 0,即经纬仪二可能不是正好位于 X 轴上。z2 的实际值与仪器误差、观测误差和 x2 有关,见下式:
z2 = x2 × tan( 仪器误差 + 观测误差) ( 3)
使用 Matlab 和数学仿真相结合的方法对测量误差进行定量分析[4]。从公式( 2) 中可以看出,经纬仪二的高度坐标 y2 未出现在公式中,对空间点的坐标测量没有影响。又从公式( 1) 中可以看出,经纬仪一的高度坐标 y1 在计算空间直线夹角时会被约减掉,对角度计算没有影响。所以在计算旋转角度时,可令仪器与待测直线位于一个水平面中,即忽略高低角 ε。在图 3 所示的模拟方位测量环境中,“OXYZ”为测量坐标系,“0' X' Y' Z' ”为液位变送器坐标系,经纬仪一位于测量坐标系原点,经纬仪二位于X 轴正向上,待测直线为液位变送器前点和后点的连线,初始位置时令其与 X 轴平行,随后绕 Y' 轴逆时针转过 α[5]。虚线所示为两台经纬仪对于前点和后点的瞄准线。设待测直线长度为 l,液位变送器与 X
轴之间的距离为 d,经纬仪二在 X 轴上的坐标为 x2 。
根据矢量代数的方法就能得到两台经纬仪对前点、后点在旋转前后的理论观测值( 见表 1) 。此时将 l,d,x2 ,α 定为一个任意的确定值,就可以根据第 1 节所述原理计算得到旋转角。
接下来将仪器误差和观测误差引入理论观测值。为使观测误差对测量结果的影响#大化,应让前后两条直线角度变化#大且方向相反,因此可按#后加入架设误差。因为有观测误差的存在,使得经纬仪二实际上并不正好位于 X 轴上。
4 结束语
本文既介绍了对液位变送器静态角度进行高精度测量的理论依据,也对这种测量方法的误差进行了定量的计算分析。这些均是作者实际工作中的经验总结,被多个项目实践证明是切实可行的,希望对今后相类似项目的研制能有一些借鉴意义。也正因为此,这些方法肯定也存在它们的局限性,或者理论模型不够准确,或者操作方法不够简便,需要更多、更进一步的工程实践来完善,更需要这方面的专家不吝批评指正。
注明,永利总站总区仪表文章均为原创,转载请标明本文地址